문제
https://www.acmicpc.net/problem/10816
10816번: 숫자 카드 2
첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드에 적혀있는 수는 -10,000,000보다 크거나 같고, 10,0
www.acmicpc.net
알고리즘
이분탐색(lower_bound, upper_bound)
풀이
이분탐색 개념의 lower_bound와 upper_bound의 개념을 알고 있는지를 확인하는 문제였다.
정렬을 시켜주고 타겟 숫자보다 큰 숫자가 나타나는 인덱스를 구하고(upper_bound) 타겟 숫자가 처음으로 진입하는 나타나는 인덱스를 구한다.(lower_bound)
그리고 upper_bound - lower_bound를 해주면 배열에서 타겟숫자의 개수를 구할 수 있다.
코드
package com.company;
import java.util.Arrays;
import java.util.Scanner;
public class Test_ParameterSearch {
public static void main(String args[]) {
Scanner in = new Scanner(System.in);
int N = in.nextInt();
int[] arr = new int[N];
for (int i = 0; i < N; i++) {
arr[i] = in.nextInt();
}
Arrays.sort(arr);
int M = in.nextInt();
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
int target = in.nextInt();
sb.append(upperBound(arr, target) - lowerBound(arr, target)).append(' ');
}
System.out.print(sb);
}
private static int lowerBound(int[] arr, int target) {
int low = 0;
int high = arr.length;
while (low < high) {
int mid = (low + high) / 2;
if (arr[mid] >= target) {
high = mid;
} else {
low = mid + 1;
}
}
return low;
}
private static int upperBound(int[] arr, int target) {
int low = 0;
int high = arr.length;
while (low < high) {
int mid = (low + high) / 2;
if (arr[mid] > target) {
high = mid;
} else {
low = mid + 1;
}
}
return low;
}
}
기본 이분탐색과의 비교
기본 이분탐색과 lower_bound, upper_bound를 구현하는데 차이점이 몇 가지가 있다.
- if(arr[mid]>target)일 때
- end=mid -1(이분탐색)
- end=mid (lower_bound, upper_bound)
- while문 조건 (등호)
- start <= end (이분탐색
- start < end(lower_bound, upper_bound)
아래에서 자세히 알아보자.
1. if(arr[mid]>target)일 때
이분탐색의 경우
1) 충분할 때 --> 등호포함
target>=arr[mid]
즉 찾고자 하는 값이 중간값보다 크거나 같으면
start=mid+1 로 하한선을 높여준다.
2) 부족할 때 -> 등호포함 x
target<arr[mid]
찾고자 하는 값이 중간값보다 작으면
end=mid-1로 하한선을 낮게 해준다.
upper_bound, lower_bound의 경우
근데 upper bound나 lower bound 는 신기하게도 end=mid만 해준다.
그 이유는 예제를 통해 설명하겠다. (upper bound만 설명해보겠다)
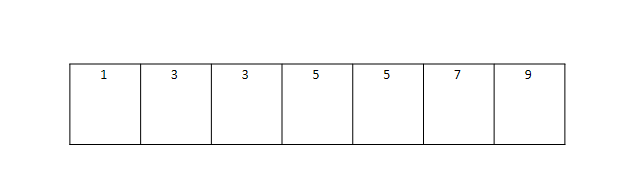
숫자카드 배열이 7개 있고, target 값이 3이다. target값의 upper bound를 찾아보자.
start=0, end =7 mid=3
3<5(arr[mid]) 이기에 end=mid 즉 end=3이다.
왜냐하면 upper bound는 찾고자하는 값보다 처음으로 큰 값이 나올때의 인덱스이기 때문에
굳이 end-1하지 않아도 end=3이 upper bound가 될 수 있기 때문이다.
실제로도 3번째 인덱스가 3의 upperbound 이다. 3-1만 해줘도 바로 컷된다.
2. while문 조건 (등호)
while (start < end)에서 왜 등호가 안붙는지 궁금했다. 다른 이진탐색은 while(start<=end) 여도 잘 돌아가는데 얘는 등호를 썼을때 에러가 뜬다.
예를 들어 while(start<=end) 일때로 가정하고 문제를 풀어보자.

7개의 숫자 배열 중 찾고자 하는 값(target 값)이 3일 때, 이 3의 lower bound를 구하는 과정을 상세히 알아보자.
start=0,end =7일 때
mid=3 그러므로 target<=5(arr[mid]) end=3
start=0 end=3 일때
mid는 1 그러므로 target<=3(arr[mid]) end=1
start =0 end =1 일 때
mid=1 그러므로 target> 1(arr[mid]) start=1
start=1 end=1일때
mid =1 그러므로 target>=arr[mid] end=1
--> end=mid-1이 아닌 end=mid 를 해줬기에 무한루프를 계속 돌거다
그래서 등호 빼줘야 한다.
++) 그리고 end값은 배열에 (n-1)번째 인덱스까지만 원소를 넣었다고 end=n-1로 해주면 안된다. 알고보니 탐색범위가 start이상 end미만 이여서 end가 원래 인덱스보다 1만큼 크게 설정해줘야한다.
결론적으로 end=arr.length라고 처음에 선언해주면 문제없이 돌아간다.
참고자료
https://we1cometomeanings.tistory.com/232
[java 백준] 실버 4/10816번 숫자카드 2
https://www.acmicpc.net/problem/10816 10816번: 숫자 카드 2 첫째 줄에 상근이가 가지고 있는 숫자 카드의 개수 N(1 ≤ N ≤ 500,000)이 주어진다. 둘째 줄에는 숫자 카드에 적혀있는 정수가 주어진다. 숫자 카드
we1cometomeanings.tistory.com
'Algorithm (PS) > 백준' 카테고리의 다른 글
| [백준] 2178. 미로탐색 (Java) [BFS 최단거리) (0) | 2023.07.11 |
|---|---|
| [백준] 1260. DFS와 BFS (Java) (0) | 2023.07.10 |
| [백준] 2805. 수들의합 (Java) [이분탐색] (0) | 2023.07.08 |
| [백준] 1789. 수들의합 (Java) [이분탐색] (0) | 2023.07.08 |
| [백준] 2346. 풍선 터트리기 (Java) [Deque] (1) | 2023.07.06 |